算法/算法分析与设计
算法23 分钟 读完 (大约 3420 个字)

算法/算法分析与设计

算法

第一、二章 基本概念

纲要

  • 循环不变式
  • 伪代码范式
  • 选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法，而冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。

Q&A

  • 算法的基本概念和性质

  • 算法是一组有穷的规则，它规定了解决某一特定类型问题的一系列运算

  • 什么是循环不变式？用循环不变关系证明循环的正确性

    • 在第一次进入循环之前成立、以后每次循环之后还成立的关系
    • 分三步走： 1）初始化：证明初始状态时循环不变式成立，即证明循环不变式在循环开始之前为真； 2）保持：证明每次循环之后、下一次循环开始之前循环不变式仍为真； 3）终止：证明循环可以在有限次循环之后终止，终止时循环不变式依然为真

第三章

纲要

  • 上界、下界、渐进紧确界：Ω、O、Θ
  • 非渐进紧确界：w、o
  • 限界函数性质：传递性、自反性、对称性、转置对称性
  • 相关定理（用于估算限界函数）：多项式定理、阶大小定理
  • 指数时间算法、多项式时间算法
  • n 较大时，大于nlogn的算法比较困难

Q&A

第四章 分治策略

纲要

  • 最大子数组问题
  • 化简递归式：代换法、递归树法、主方法
    • 代换法：预处理、猜测解、数学归纳法证明
    • 递归树法：预处理、画递归树、求极限和、数学归纳法证明
    • 运用主定理
    • 展开法直接化简

Q&A

  • 分治法的基本思想
    • 当问题规模比较大而无法直接求解时，将原始问题分解为几 个规模较小、但类似于原始问题的子问题，然后递归地求解这些 子问题，最后合并子问题的解以得到原始问题的解。
    • 分解、解决、合并

第八章 线性时间排序

纲要

  • 最坏情况下，任何排序算法都要进行Ω(nlgn)次比较
  • 桶排序、归并排序为渐进最优排序算法，时间复杂度为f(n)=O(nlgn)

第十五章

纲要

  • 经典问题

    • 钢条切割问题 O(n2)O(n^2)
    • 矩阵链乘 O(n3)O(n^3)
    • 最长公共子序列问题LCS O(nm)O(nm)
    • 最优二叉搜索树 O(n3)O(n^3)

  • 估算时间复杂度

    • 子问题图法：Σ所有结点结点出度Σ_{\text{所有结点}}\text{结点出度}
    • Σ所有子问题解决一个子问题要用的操作数Σ_{\text{所有子问题}}\text{解决一个子问题要用的操作数}

  • 最优子结构和子问题无关性

    • 最长简单路径不满足子问题无关性

  • 剪切-粘贴法

Q&A

  • 最优化问题是一类什么问题？
  • 这一类问题的可行解可能有很多个。每个解都有一个值，我们希望寻找具有最优值的解（最小值或最大值）
  • 简述对动态规划所能带来计算性能改进的理解
    • 备份子问题的解，空间换时间
  • 什么是状态转移方程
    • 即问题状态的递推关系式

第十六章 贪心算法

纲要

  • 基本思想
    • 分步骤实施，它在每一步仅作出当时看起来最佳的选择，即局部最优的选择，并寄希望这样的选择最终能导致全局最优解，（贪心选择性质）
  • 经典问题
    • 最小生成树问题的Prim算法、Kruskal算法，单源最短 路径Dijkstra算法等，以及一些近似算法
    • 活动选择问题 O(n)O(n)：每次选择最早结束的活动加入集合
    • 哈夫曼编码：每次移除队列中频率最低的两个结点合并成一个结点加入队列
  • 尾递归可以轻松地转化为循环式
  • 可以解决分数背包问题 O(nlogn)O(nlogn)，不能解决0-1背包问题

Q&A

  • 贪心算法的基本思想和一般步骤

    • 基本思想：通过选择局部最优来导致全局最优
    • 确定问题的最优子结构；
    • 将最优化问题转化为这样的形式：每次对其作出选择后，只剩下一个子问题需要求解；
    • 证明作出贪心选择后，剩余的子问题满足：其最优子解与前面的贪心选择组合即可得到原问题的最优解(具有最优子结构)。

  • 什么是贪心选择性和贪心选择?

    • 贪心选择性质：可以通过做出局部最优（贪心）选择来构造 全局最优解的性质。
    • 在贪心算法的每一步所做的当前最优选择（局部最优选择）就叫做贪心选择

  • 比较动态规划和贪心方法的异同。

    • 贪心算法可以直接进行贪心选择，而动态规划必须要比较各种选择决出最优选择
    • 贪心算法和动态规划都需要问题满足最优子结构和子问题无关性

第二十章 基本的图算法

纲要

  • 邻接表、邻接矩阵

  • BFS、DFS

  • 活结点、E-结点、死结点

  • 回溯法

    • 使用限界函数的深度优先状态结点生成方法称为回溯法

  • 分支-限界法

    • 使用限界函数的E结点一直保持到死为止（中间不会经历活结点状态）的状态结点生成方法称为分支-限界方法（宽度优先）
      • 两种策略——FIFO检索：活结点表采用队列、LIFO检索：活结点表采用栈
    • LC检索(A*算法)
      • 选择C^(X)\hat{C}(X)值最小的活结点作为下一个E-结点的状态空间树检索方法
      • 成本估计函数 C^(X)=g^(X)+f(h(x))\hat{C}(X) = \hat{g}(X) + f(h(x))
      • C(X)C(X) 成本函数，只有当整个状态空间树生成出来时才知道
      • g^(X)\hat{g}(X) 是由X到达一个答案结点所需成本的估计函数
      • h(X)h(X) 是根节点到X的成本——已发生成本
      • f(X)f(X) 是某一个不减函数
      • BFS和D_Search是特殊的LC检索，对于BFS有 g^(X)=0\hat{g}(X)=0，f(h(x))=f(h(x))= 结点深度；对于DSearch有f(h(x))=0f(h(x)) = 0，XX越深g^(X)\hat{g}(X)越小
    • 利用分支限界法求解最优化问题
      • 利用成本估计函数（成本下界）C^(X)\hat{C}(X)智能地选择下一个E-结点
      • 成本上界UU由答案结点的成本C(X)C(X)所更新，扩展结点时舍去 C^(X)>U\hat{C}(X) > U 的结点
      • 典型例题：带限期的作业排序问题

Q&A

  • BFS、DFS、D_Search的区别

  • 简述 LC-检索的基本思想

    • 选择成本估计最小的活结点作为下一个E-结点的状态空间树检索方法，以此来加快找到一个可行解

  • 什么结点成本函数和结点成本估计函数？结点成本估计函数中h函数和𝑔̂函数会分别对算法带来什么影响？

    • 结点成本函数是指经过该结点到达可行解的最小实际成本
    • 结点成本估计函数是对结点成本函数的估计
    • h(X)h(X)函数使得算法优先考虑距离答案结点更近的结点作为下一个活动结点
    • g^(X)\hat{g}(X) 函数使得算法优先考虑离根结点更近的结点（已发生成本更低）

  • 了解𝑔̂函数的性质，了解C(X)上界的作用

    • 单纯使用g^(X)\hat{g}(X)选择E结点会导致算法偏向纵深检查
    • C(X)上界能够杀死那些明显成本更大活结点，加速算法，降低检索的盲目性

第二十三章 最小生成树

  • 最小生成树的生成

第二十四章 单源最短路

纲要

  • 基本概念
    • 前驱子图 Gπ(Vπ,Eπ)G_\pi (V_\pi, E_\pi)，最短路径树（算法终止后的最终 GπG_\pi）
      • 即VπV_\pi是图G中的前驱结点不为NIL的结点的集合，再加上源点s
      • 即EπE_\pi是由VπV_\pi中的结点的π\pi值所“诱导”的边的集合
    • 前驱节点 v.πv.\pi，最短路径长度上界 v.dv.d
    • 最短路径的最优子结构：两个结点之间的最短路 径的任何子路径都是最短的。
    • 如果存在负权重的边，则有可能存在权重为负值的环路， 而造成图中最短路径无定义。
    • 最短路不应包含环路：简单路径
  • 算法证明
    • 路径松弛性质：Relax(u,v,w)Relax(u, v, w) 后有 v.d≤u.d+ω(u,v)v.d \leq u.d + \omega (u,v)
    • 三角不等式性质 δ(s,v)≤δ(s,u)+ω(u,v)\delta (s, v) \leq \delta (s, u) + \omega (u, v)
    • 上界性质 δ(s,v)≤v.d\delta (s, v) \leq v.d
    • 收敛性质：松弛操作 relax(u,v)relax(u,v) 前有 u.d=δ(s,u)u.d = \delta (s, u) 则松弛后必有 v.d=δ(s,v)v.d = \delta (s, v)
  • Bellman-Ford 算法 O(VE)O(VE)
    • 可以有负权重的边，但不能有负权重的环
  • Dijkstra 算法
    • 不能有负权重的边和环
    • 时间复杂度：
  • 差分约束系统

    • 约束图

      • 边的权重：如果 xj−xi≤bkx_j - x_i \leq b_k 是一个差分约束条件，则边 (vi,vj)(v_i ,v_j) 的权重记为$ ω(v_i ,v_j ) = b_k$ ，而从v0v_0出发到其他结点的边的 权重 ω(v0,vj)=0ω(v_0 ,v_j)=0

    • 问题归约

      • 如果图G不包含权重为负值的回路，则 (δ(v0,v1),δ(v0,v2),...,δ(v0,vn))(\delta (v_0, v_1), \delta (v_0, v_2), ..., \delta (v_0, v_n)) 为差分约束系统的一个可行解（用三角不等式证明）
      • 如果图G包含权重为负值的回路，则该系统没有可行解

Q&A

  • 什么是松弛操作？
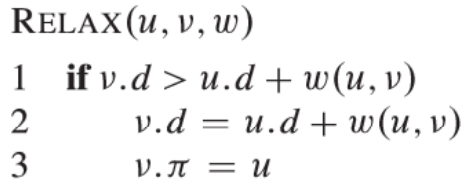
  • 举例说明在带有负权重边的图上 Dijkstra 算法工作异常。
  • Bellman-Ford 算法是如何检查图中可能存在的负权重回路的？
    • 对每条边松弛迭代V-1次之后，检查所有边 (u,v)(u,v) 看看是否有 v.d>u.d+w(u,v)v.d > u.d + w(u,v)，如果有说明存在负权重回路，否则不存在。

第二十五章 多元最短路

纲要

  • 成本邻接矩阵W，最短路径矩阵D，前驱结点矩阵Π
  • Floyd-Warshall 算法 O(v3)O(v^3)
    • 算法允许图中存在负权重的边，但不能存在权重为负值的环路
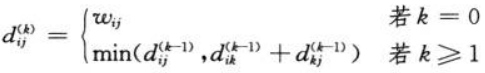
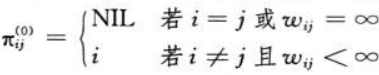
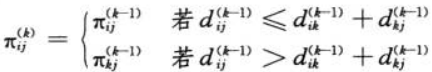
    • 特殊应用：计算传递闭包T（min=>∨min=>\lor 、+=>∧+ => \land）
  • Johnson 算法 O(n3)O(n^3)
    • 用于稀疏图
    • 重赋权重+单源最短路法： 如果图G包含权重为负值的边，但没有权重为负值的环路， 则通过重赋权重，构造出一组新的非负权重值，然后通过对每个结点运行一次Dijkstra算法来找到所有结点对之间的最短路径
    • 新权值 w^\hat{w} 要满足路径等价性和非负性
    • w^(u,v)=w(u,v)+h(u)−h(v)\hat{w} (u,v) = w(u,v) + h(u) - h(v)，其中 h(u)=δ(s,u),h(v)=δ(s,v)h(u) = \delta(s, u), h(v) = \delta(s, v)，ss 为辅助点且满足 w(s,v)=0,v∈Vw(s,v) = 0, v \in V
    • 算法思想：
      • 先用Bellman-Ford算法计算s到各个结点的最短路径，并判断是否存在负权重的环路
      • 利用Bellman-Ford算法计算得到的δ(s,v)定义h(v)的值，并重新赋边的权重
      • 还原路径权重，得到原图的路径权重矩阵D

第二十六章 最大流

纲要

  • 流网络

    • 是一个带有源/汇点，每条边带有容量限制的有向图 G(V,E)G(V,E)
    • 流网络是连通图
    • 不允许自循环

  • 流的性质

    • 容量限制：0≤f(u,v)≤c(u,v)0 \leq f(u,v) \leq c(u,v)，ff为实际流量，cc为容量，u,v∈Vu,v \in V
    • 流量守恒：除了源/汇点之外的点流入和流出的流量大小相同

  • 标准流网络：无反向平行边，单一源/汇点

  • 一般流网络标准化方法：新增结点法

    • 对于反平行边，引入结点将其截断
    • 对于多个源/汇点，引入一个超级源/汇点，令其到原来的源/汇点的容量限制均为∞

  • Ford-Fulkerson 算法步骤

    • 对流网络 GG，在残存网络 GfG_f 中寻找一条增广路径 pp。
    • 如果存在增广路径，则对路径上边的流量进行修改，以增加流网络的流量。
    • 重复这一过程，直到不再存在增广路径为止。

  • 流网络的切割

  • Edmonds-Karp 算法

    • 找增广路径时采用广度优先搜索策略

  • 最大二分匹配

    • 新增源/汇点
    • 所有边容量为1

Q&A

  • 什么是流网络、最大流？
  • 最大流最小切割定理
    • 以下三个条件等价:
    • f是G的一个最大流
    • 残存网络不包括任何增广路径
    • ∣f∣=c(S,T)|f|= c(S,T) ，其中(S,T)是流网络G的某个切割
  • Edmonds-Karp 算法的思路和相关证明
#

喜欢这篇文章？打赏一下作者吧

×