技术/笔记/离散数学笔记

Math 课程笔记

计数技术基础

乘法原理与笛卡尔积的基数

|A1 ⨉ A2 ⨉ ∙∙∙ ⨉ Am |= |A1| ∙ |A2| ∙ ∙∙∙ ∙ |Am|

容斥原理

有根树图

鸽巢原理

• 推论：一个从m个元素到n个元素（m>n)的函数不可能是单射。
• 广义鸽巢原理
  • 如果N 个物体放置到k个盒子中，那么至少 有一个盒子装有不少于⌈N/k⌉个物体。
  • 关键词：至少，分配（/填色/分类）
  • 要用上鸽巢原理就要灵活转换问题
• 可用结论：
  • 任何一个正整数都给可以分解为一个2的次幂×一个奇数

排列组合

乘法原理，加法原理，组合，排列

二项式系数与组合分析法

组合分析法证明

允许重复的n元素的r排列

$n^r$

允许重复的n元素的r组合

$C_{n+r-1}^r$

思想：隔板选位，不定方程求解

可分辨与不可分辨的分配问题

将n个可以辨别的物体（或者说n个不同的物体）放入到k 个可以辨别的盒子里，使得第i个盒子有ni个物体，有：n!/(n1!n2! ∙∙∙nk!) 种方法，多的可以认为全都放到第k+1个盒子里！

proof：分类组合

不可分辨的物体放入可分辨的盒子里：不定方程问题

$C_{n+r-1}^r$

递推关系

线性齐次递推关系通解形式

$a_n=\sum^i C_in^kr^n$

$C^i$为待定常系数，r为特征根，k依据重根数决定（例如二重根$r_1, r_2$，对应项$C_1r^n, C_2r^n$）

线性非齐次递推关系特解形式

如果f(n)为n次多项式，则特解一般也是n次多项式

F(n)为指数函数$\beta^n$，若$\beta$不是特征根，则有特解为 $H^*(n) = P\beta^n$
其中P为待定常数.

若β是e重特征根，则特解为$Pn^e\beta^n$

生成函数

表示序列的一种有效方法是生成函数，它把序列的项作为 一个形式幂级数中变量x幂的系数。这样的生成函数可以 用来求解许多类型的计数问题，诸如

• 在各种限制下选取或分配不同种类的物体的方式数；

• 用不同面额钱币构成某个数额的钱的问题；

• 求解某些带限制条件的不定方程的问题等等。

• 整数分解问题

• 用生成函数求解特殊的递推关系

值得注意的是：利用生成函数解决问题关注的是幂级数的形式，幂级数是否收敛不重要。利用生成函数的性质（比如展开成幂级数，幂级数求导与积分）可以方便地用来求解计数问题。

生成函数分析法

常用函数的幂级数展开式

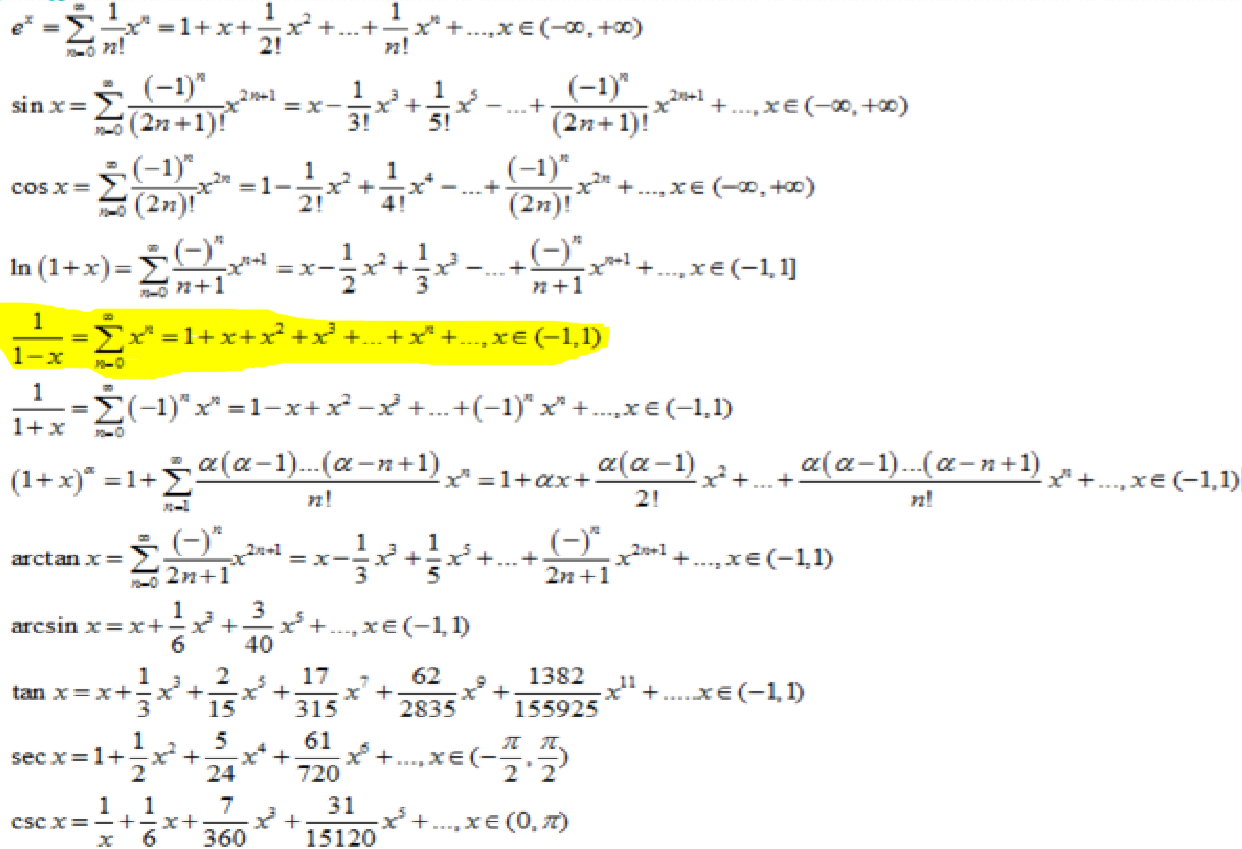
广义二项式

常用结论

$G(n)=\frac{1}{(1-x)^n}=\sum_{r=0}^∞C(n+r-1, r)x^r$

生成函数求解不定方程解的个数

应用

转化为不定方程解的个数求解问题

容斥原理

• 第二形式：N(P′1P′2 . . . P′n) = N − |A1 ∪A2 ∪ · · · ∪An|
  • $A_i$标识包含属性$P_i$的集合
• 错位排列

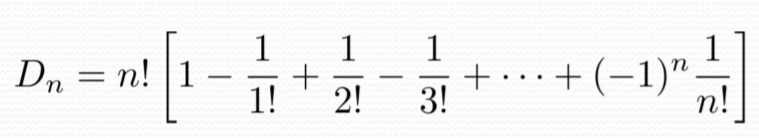
模余运算

同余运算性质

---

if a ≡ b (mod m) & c ≡ d (mod m)

then a+c ≡ (b+d) (mod m) & ac ≡ bd (mod m)

(m为正整数)

---

$a \equiv b (mod\space m) \Rightarrow ca \equiv cb (mod\space m)\space (c \in Z)$

$ca \equiv cb (\text{mod}\space m)\space \Rightarrow a \equiv b (\text{mod}\space m)\space (gcd(c,m) = 1)$

---

和、积的模

(a + b) mod m = ((a mod m) + (b mod m)) mod m
ab modm = ((a modm) (b mod m)) mod m

(m为正整数)

最大公因子

• gcd(a, b)是a，b的线性组合
• 求法：
  • 素数分解
  • 辗转相除法

同余方程

解线性同余方程

ax ≡ b (mod m)

模逆

• $\bar aa = 1\space (m)$

• 模逆存在唯一性定理：$gcd(a, m) = 1,\space m > 1$则a关于模m的模逆存在且正唯一

• 求模逆

  • a, m 辗转相除，倒回去写成1 = sa + km的形式，s即为模逆

可求模逆的方程解法

• 求模逆
• 两边同乘模逆消掉系数a
• 得出结论

欧拉函数

1到n范围内与n互素的数的集合叫做欧拉函数单元的集合（units），其数量为欧拉函数Φ(n)

性质

• p, q为素数

• $\Phi(n)(p) = p − 1$

• $\Phi(pq) = pq − (p + q − 1) = (p − 1)(q − 1)$

欧拉定理

• 欧拉定理: $a^{\Phi(n)} \equiv 1 \space (\text{mod} \space n)$ (a是n的一个unit)
• Fermat Little Theorem： $a^{p-1}=1 (mod\space p)$ (p是一个素数 && p不能整除a)
• $a^p\equiv a(\text{mod}\space p)$ (p是一个素数 && a为任意整数)

RSA加密解密

素数p，q，有$\phi(pq)=(p-1)(q-1)$，令$M=pq$，$ed\equiv 1(mod \space M)\equiv 1(mod \space(p-1)(q-1))$

记明文为P，密文为C

• 接收方选择好p，q，e然后计算好M，d发送出去
• 发送方接受(M, d)并发送密文$C\equiv P^d\space (\text{mod}\space M)$
• 接收方解密$P\equiv C^e\space (\text{mod}\space M)$